The Elliptic Curve Digital Signature Algorithm

타원곡선 DSA(ECDSA)는 타원곡선을 이용한 전자서명 알고리즘이다.

타원곡선(Elliptic Curve)

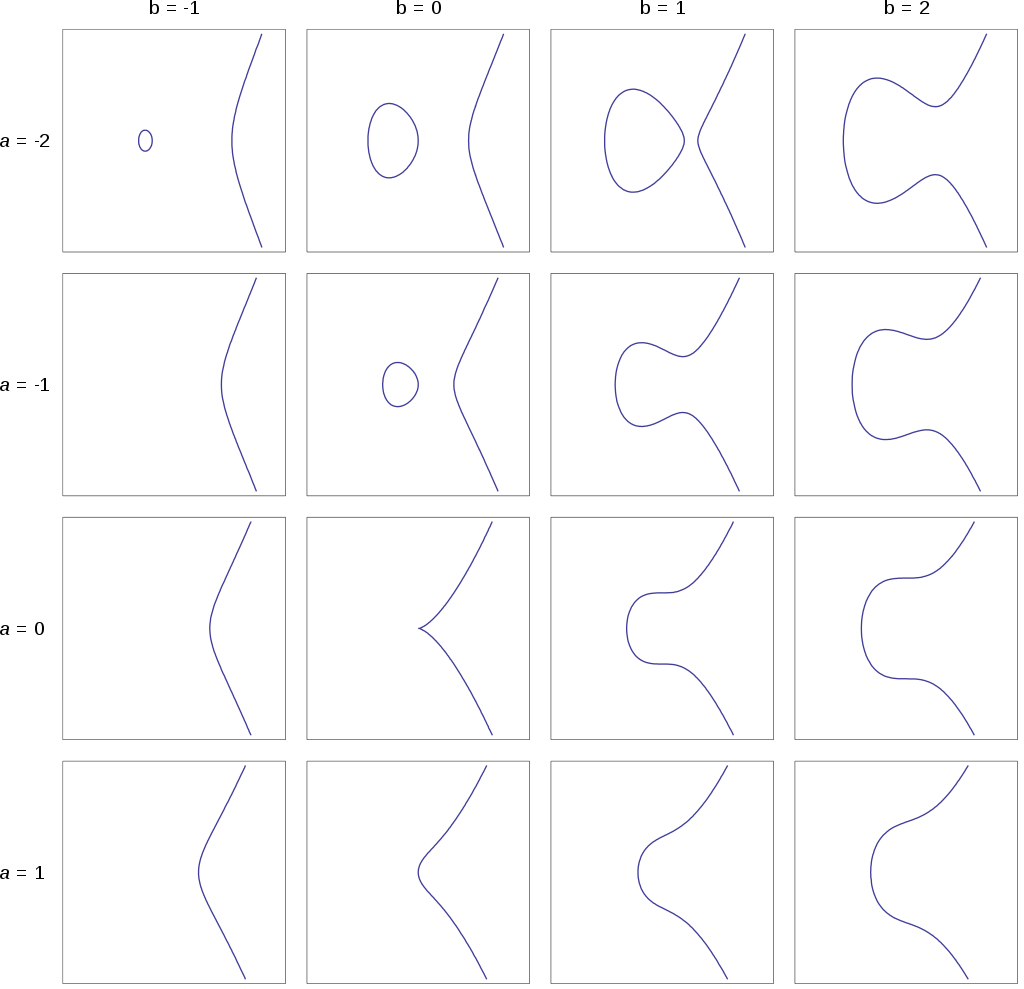
y^2 = x^3 + ax + b 형태의 방정식으로 정의대는 대수 곡선으로서, 첨점이나 교차점 등의 특이점이 없는 것이 특징이다.

Addition

Geometric Approach

P + Q = R, P ≠ Q

P + P = 2 P = R

Algebraic Approach

P=(x1,y1) ∈ E, Q=(x2,y2) ∈ E , P + Q = (x3,y3) [P!=Q]

P=(x1,y1) ∈ E, P != -P, then 2P = (x3,y3)

Galois Fields GF(q)

g 가 소수라면 Zg는 field이다. ex)Z5,Z7,Z11,…

Z7 = {0,1,2,3,4,5,6}

Z7 = {0,1,2,3,4,5,6}
+:
1 + 3 = 4
5 + 6 = 11 mod 7 =4
identity of +:
2 + x = 0, x = 5 (7 mod 7 = 0)

-: inverse of +

identity of *:
2 * x = 1, x = 4 (8 mod 7 = 1)
3 * x = 1, x = 5 (15 mod 7 = 1)
4 * x = 1, x = 2 (8 mod 7 = 1)
5 * x = 1, x = 3
6 * x = 1, x = 6

Z5 = {0, 1, 2, ,3, 4}
2^-1 = 3 (6 mod 5 = 1)
3^-1 = 2 (6 mod 5 =1)
4^-1 = 4 (16 mod 5 =1)

a,b ∈ Z5일 때

• a + b mod 5 = {(a mod 5) + (b mod 5)} mod 5 이다.

• ab mod 5 = {(a mod 5)(b mod 5)} mod 5 이다.

a = qn + r1, b = q’n + r2 일때

a*b mod n = {(q*q’)n^2 + (r1*q’ + r2*q)n + r1*r2} mod n이다.

즉, [ab mod n = r1r2 mod n = {(a mod 5)(b mod 5)} mod 5] 가 성립한다.

타원곡선 E: y^2 = x^3 + x + 4 의 경우

x=0일때 y^2=4이므로 y=2,3((-2+5)mod5 = 3)이다.